I’m so sad to see this sweet couple’s time with me come and go. We hit it off from the get go. Shelby and Colby have such fun personalities and they don’t meet a stranger. Between Colby and I’s love for LSU, how we all three have crazy love for our dogs, and all the fun conversations in-between, I’ve felt like Shelby, Colby, and I have been friends from the start. They embraced the insane winds during their engagement session, it actually started pouring during Shelby’s bridals, but on their wedding day, we couldn’t have asked for more perfect weather. I was thrilled to wake up the morning of their wedding and drive 8 miles down the road to the beautiful Orchard at Caney Creek wedding venue in Wharton. It was absolutely stunning. I wish the Smiths a lifetime of love and happiness, and I’m honored they chose me to photograph one of the most important days of their lives.





















































































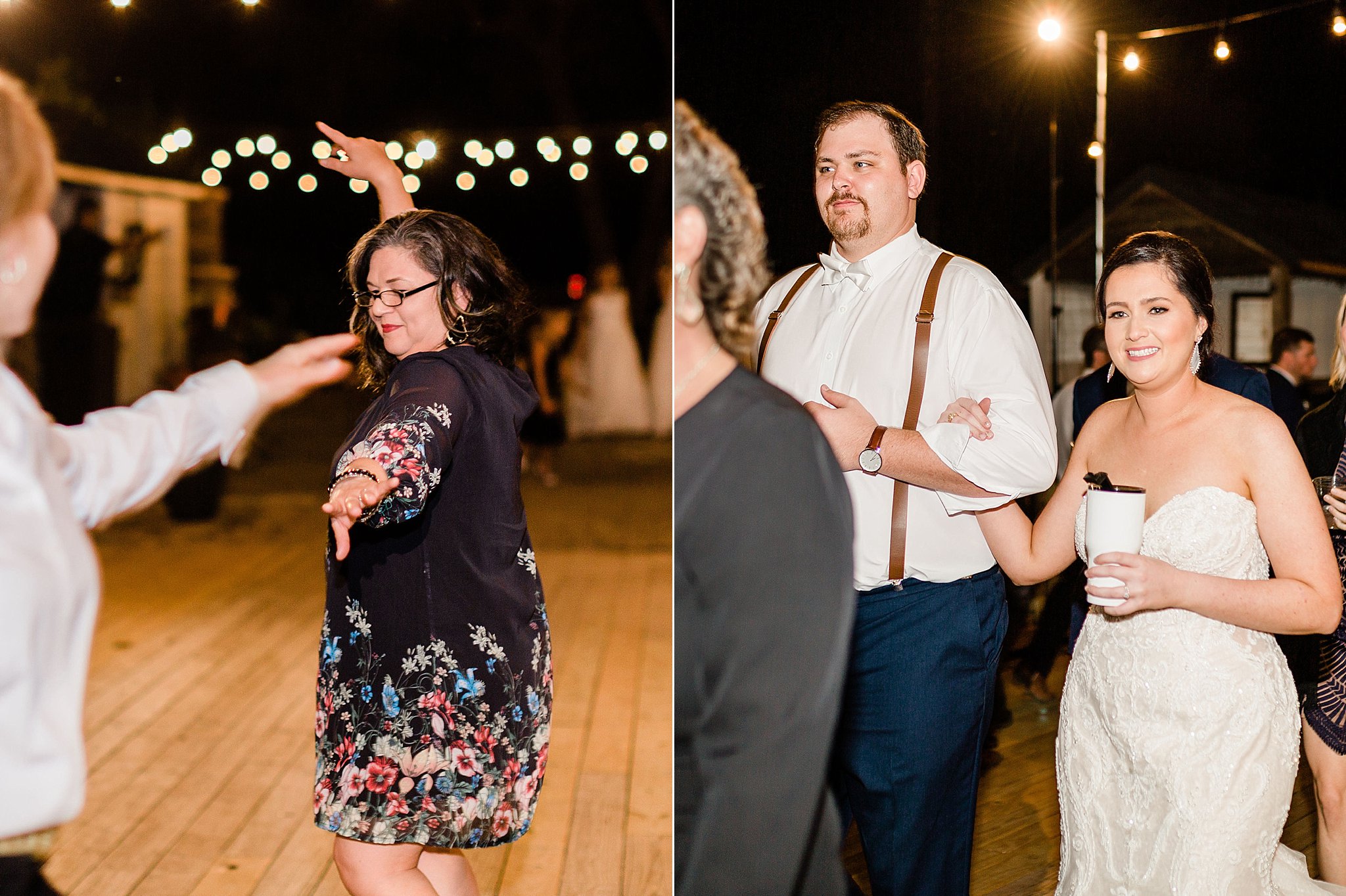


Beautiful photos!
Becka, you truly outdid yourself. We absolutely love them – couldn’t have asked for a better person to capture our special day!
Becka- I love them all so much! You’re amazing!
And Shelb- you and your wedding were simply gorgeous!
Such a beautiful wedding! And beautiful photos to remember this day forever!
Beautiful pictures with great quality! Awesome job!
Wonderful photos!!!
The pictures are beautiful and captured Colby and Shelby’s special day perfectly!
Amazing photos!!! Loved them all❤️
Amazing photos! Love them all❤️
Such incredible photos!!!
Becka you are truly amazing and so much fun to work with! Thank you for capturing all of the special memories so perfectly.
Such incredible photos!!
Beautiful wedding pics!
So gorgeous!
I hope my wedding is as beautiful as yours one day! Congratulations!!
So many amazing moments captured ! Very Beautiful!
These are just beautiful!
Beautiful!
Such a fun day! Great pics…we all had a blast!!
Wonderful memories for a wonderful time. cherish every one of them.
These are beautiful pics. Congratulations to both of you! Best wishes for many years!!!!
What a beautiful wedding and family. Love every detail!
just beautiful!
Beautiful pictures
The photos are breathtaking!! What a joyful day! Congratulations to the new Mr. and Mrs. Colby Smith! May God richly bless your marriage!
Absolutely Beautiful!
Great photos
The pictures are stunning. I love how she captured the people and the background was just that-background. Beautiful!!!!!
Absolutely Beautiful Wedding Pictures!
Beautiful pictures of a lovely wedding. Much happiness to you both!
Beautiful pictures of a beautiful day. Congratulations Colby and Shelby.
So much fun and so much love!!! The pictures are stunning!
Beautiful!
A beautiful wedding – Shelby was nothing less than stunning!
Wishing you both many, many years of health and happiness.
Congratulations!
Such beautiful photos of Colby and Shelby’s special day! Love how they truly capture the joy and love of the day. I particularly like the black & white photos and the photos that capture the images up close and fade in the distance. Congratulations Colby and Shelby! Wishing you a lifetime of love, laughter and adventure!
Awesome photos!!! It was a beautiful
wedding!
What a great wedding. The photos are wonderful and caught so much of what happened at the wedding. These are the type of photos that will last more than a lifetime.
Absolutely gorgeous.
Most beautiful photos for the most beautiful couple. Congratulations Mr. & Mrs. Smith.
Awesome pics! You did such a great job capturing a beautiful wedding!!
Becka, I truly cannot say enough positive words about you and your work. This perfect day looks just as amazing in pictures as it did in person. The Smiths make such a beautiful couple!!
Amazing day and amazing photographer!!
Absolutely gorgeous!! So glad I was able to witness such a wonderful day!
These photos truly do a great job of capturing such a perfect day!
Amazing pictures! Awesome photographer!! Mindi you look Amazing!!!!
Absolutely gorgeous!
What a beautiful couple! Best Wushes!
Very beautiful photos!
Superb job at capturing so many memorable moments of such a beautiful couple and their special day! Exquisitely done!! Can’t wait to see more!!
What an exquisite wedding wishing much happiness to Shelby and Colby. The photos are absolutely beautiful what memories.
Good pictures
Beautiful pictures for a beautiful couple
What a beautiful day it was! Wishing Colby and Shelby all happiness and what amazing pictures!!
I was there at the wedding and I thought it was great
Beautiful!
Gorgeous pictures of a gorgeous wedding.
What a gorgeous wedding!
What a happy couple! Venue is awesome!
Great pictures!
Lovely memories
The Snyders and the Smiths are truly blessed and must be super proud! Congratulations on your beautiful day and the blessed future which awaits you!
Looks like a Great wedding, love the pictures and the backgrounds!
Beautiful pictures and beautiful wedding party. The bride and groom were gorgeous.
It was a gorgeous day captured perfectly!
Niceeee. Pics and comments are rad.
Love all the photos.
beautiful pictures
Great pictures of an awesome couple on their wedding day.
Absolutely beautiful. Enjoyed decorating
Super cute photos!
Beautiful pictures of a beautiful couple. Congratulations and all the best for a bright future together.
Gorgeous Pics…great Job! When my kids get married (non of them are dating) you will be the photographer! You are Truly Gifted!!!
Regards,
Rhonda
Absolutely beautiful wedding and such gorgeous pictures!! Perfect day altogether!
Absolutely beautiful pictures, and a beautiful day!!
They are such good pictures! It was a beautiful day.
Caney Creek is such a beautiful backdrop to share the love between two best friends!
Absolutely a beautiful wedding and the photos surely captured it all. So glad to have been there to witness a wonderful day.
These are amazing pictures, for an amazing couple!
These are all great, beautiful wedding!
The pictures are so gorgeous ! Almost felt like I was there ❤️
Beautiful!!
Beautiful
Great photos and beautiful wedding❤️
Beautiful photos of a beautiful wedding!
Beautiful pictures of a beautiful day!
One of my most favorite and the most beautiful, picture perfect weddings I’ve ever been to. Simply gorgeous!!! Love you Shelbs and Colby.
Wonderful photos of a beautiful day!
Great pictures!!
Love these pictures, they will last a lifetime!
This is such a beautiful wedding, love the photos!
Wow, what an incredible day! Amazing pictures!
Stunning pictures, congratulations!
Beautiful photos for a beautiful day!
Gorgeous photos!
Congrats guys, y’all look great!
Some of the best photos I’ve seen!!!
Amazing photos!
Awesome job – everyone looks amazing
Lovely photos of a lovely couple. Best wishes to y’all!
Absolutely beautiful!
Such beautiful pictures
Absolutely stunning – couldn’t have asked for a better day!
Stunning – what an amazing keepsake.